Benoît Gibson
Xenakis se réfère à la notion de groupe principalement dans deux contextes différents. D’une part, pour établir la structure d’ordre des caractéristiques sonores —Xenakis légitime ainsi la correspondance entre nombres et hauteurs, qui sert de fondement à la théorie des cribles ; et, d’autre part, pour explorer les symétries propres aux structures des groupes finis. Xenakis emploie pour la première fois les systèmes des symétries des groupes lorsqu’il compose Akrata (1964), au moment où se précisent les notions de « hors-temps », de « temporelle » et d’« en-temps », qu’il définit à propos de la « musique symbolique » (Xenakis 1963, 185-208). Le recours à la théorie des groupes marque une nouvelle étape dans la démarche compositionnelle de Xenakis. Alors que la musique stochastique repose sur l’indéterminisme, les structures de groupe organisent des éléments préalablement définis selon un ordre spécifique.
Un groupe G se définit comme un ensemble d’éléments pour lequel une loi de composition vérifie les propriétés suivantes (voir Ledermann 1964, 2) :
- Fermeture : pour deux éléments quelconques A et B de G, il existe un unique élément C de G, noté C = A * B, appelé le produit de A et B.
- Loi de l’associativité : le produit de trois éléments quelconques A, B et C de G vérifie que (A * B) * C = A * (B * C).
- Élément neutre : G possède un élément I, appelé élément neutre, tel que pour chaque élément A de G, A * I = I * A = A.
- Élément inverse : à chaque élément A de G correspond un élément inverse A-1, tel que A * A-1 = I.
Très souvent, Xenakis cherche à inclure les processus compositionnels existants dans des catégories plus générales et plus abstraites. Il n’est donc pas surprenant qu’il se réfère à l’ensemble qui contient les quatre formes mélodiques (original (O), rétrograde (R), inverse (I) et inverse rétrograde (IR)) comme un exemple de structure de groupe (Xenakis 1990, 17-18). Le résultat du produit de deux formes quelconques engendre une forme du groupe (fermeture). La forme originale d’une autre forme quelconque maintient celle-ci inchangée. Elle correspond à l’élément neutre : le produit (O * IR), tout comme (IR * O), vaut (IR). Chaque forme est son propre inverse : les produits (O * O), (R * R), (I * I), (IR* IR), valent (O) (élément neutre). Enfin, les quatre transformations d’une ligne mélodique vérifient que ((O * R) * IR) = (O * (R * IR)) = I.
L’ordre du groupe est défini par le nombre de ses éléments. Les formes mélodiques (O), (R), (I), (IR) forment un groupe d’ordre 4, connu sous le nom de « groupe de Klein ». Pour un groupe d’ordre 4, il existe 16 produits distincts, qui peuvent être représentés par une table de multiplication (matrice) où chaque élément est assigné à une colonne et à une ligne.
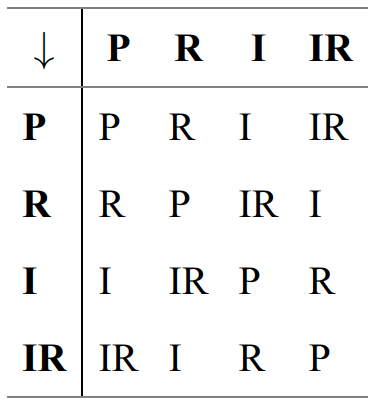
Le résultat du produit de deux éléments se trouve à l’intersection de la colonne et de la ligne correspondantes : (R * IR) ➞ (I). Il serait possible d’adjoindre à ces quatre formes les 12 transpositions du total chromatique, formant ainsi un groupe d’ordre 48. Les transpositions s’additionnent alors sous forme d’indices modulo 12. Ainsi, le produit des transformations (IR7) et (I5) vaut (R0) : (IR * I = R et (7 + 5) = 12(mod12) = 0. Xenakis utilise des figures mélodiques comme éléments de structures de groupe dans Nomos Gamma (1967).

Excerpt from Nomos Gamma (1967), mm. 203–205
Les figures mélodiques jouées par les hautbois entre les mesures 203 et 205 reposent sur la suite d’intervalles de hauteur suivante, en quarts de ton :
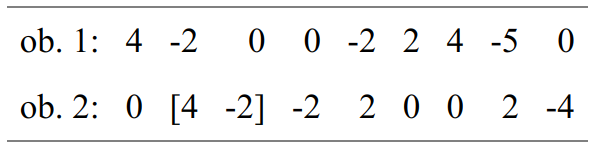
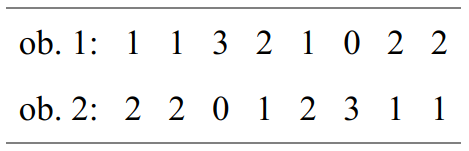
Si l’on exclut un écart au début (indiqué entre parenthèse), la ligne du second hautbois suit la forme inverse rétrograde de la suite d’intervalles du premier hautbois. Il en est de même pour les profils dynamiques. Le contour dynamique du deuxième hautbois correspond à la forme inverse rétrograde du contour dynamique du premier. Pour ce qui est des durées et des modes de jeu (stacc., flatt., quilisma), ils apparaissent sous la forme rétrograde, mais avec des unités de durée différentes : quintolets de croches pour le premier hautbois, contre croches pour le second :
Les formes géométriques et les figures peuvent être organisées selon les principes des groupes abstraits. Mais dans l’œuvre de Xenakis, le recours à la théorie des groupes se manifeste surtout pour engendrer des cycles de permutations. Ce que l’on sait de l’usage que fait Xenakis des structures de groupe nous vient surtout de son analyse de Nomos alpha (1965-1966). Les permutations correspondent à des processus de transformations notés par une suite ordonnée de nombres entiers. Chaque élément comporte une double signification : d’une part, la position qu’il occupe à l’intérieur de l’ensemble, déterminée par son rang, et, d’autre part, sa valeur numérique. La permutation (1234) maintient l’ordre des éléments inchangé́, peu importe leur valeur. Celle notée (1324) dispose les éléments dans l’ordre indiqué par les nombres entre parenthèses. Appliquer la permutation (1324) à l’ensemble {bdce} produit le résultat : {bcde}. La permutation notée (1234) maintient l’ordre des éléments inchangé́. Au sein d’un groupe, elle tient lieu d’élément neutre (identité).
Le nombre de permutations possibles de n éléments égale la factorielle de n (n! = 1 x 2 x 3 x … (n − 1) x n). L’ensemble de ces permutations forme un groupe. Leur nombre (n!) indique l’ordre du groupe. La matrice ci-dessous, tiré de l’article « Vers une philosophie de la musique » (1992, 221), reproduit la matrice d’un groupe isomorphe à celui des rotations du cube autour de ses axes de symétrie.
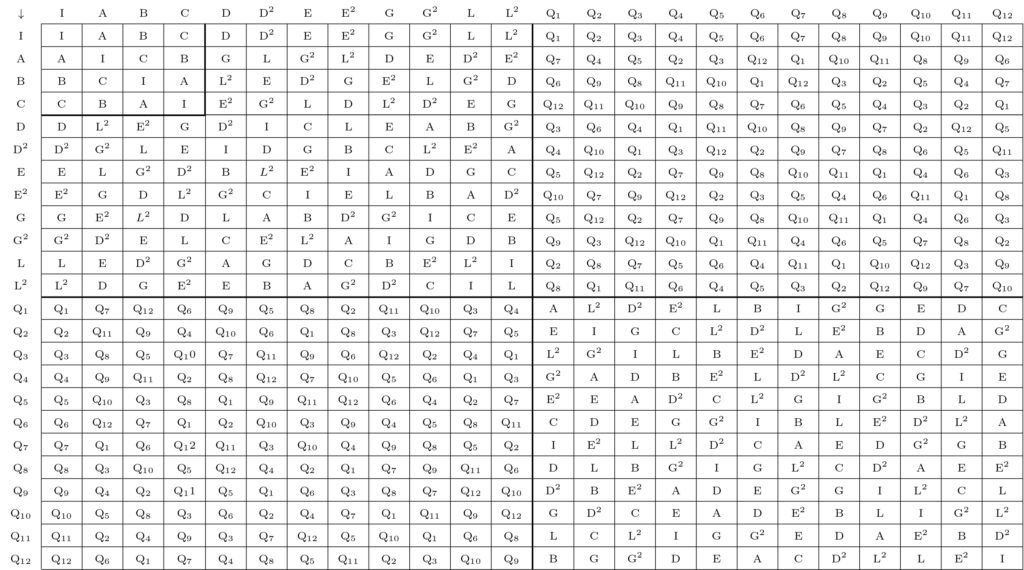
Matrix of the symmetric group P4
Ce groupe permute 8 éléments identifiés aux huit sommets d’un cube. Le tableau suivant énumère la liste des symboles associés à chaque permutation.
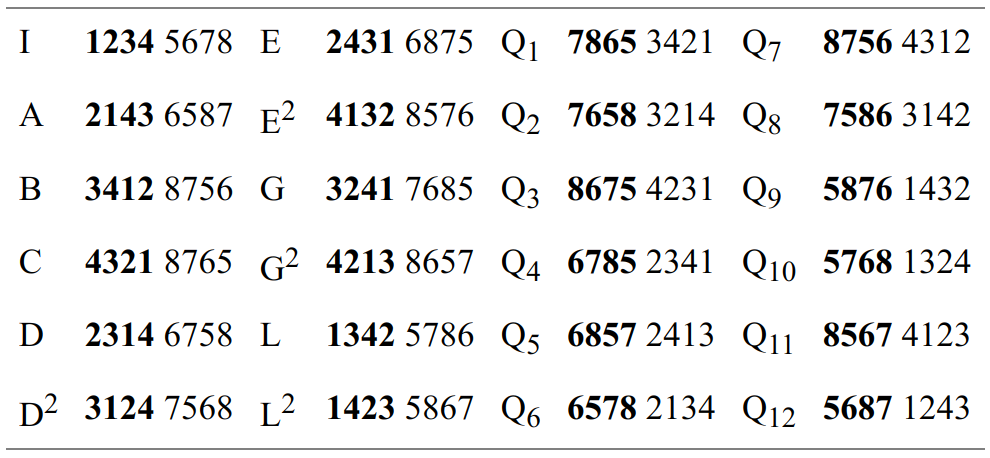
Comme pour la matrice précédente, le produit de deux transformations quelconques figure à l’intersection de la colonne et de la ligne correspondantes : le produit des transformations (D) et (A) vaut (G) : (D * A) ➞ (G). Notons que ce groupe n’est pas commutatif : (D * A) ≠ (A * D).
Le groupe des rotations du cube autour de ses axes de symétrie est isomorphe au groupe P4, c’est-à-dire au groupe qui contient toutes les permutations de 4 éléments. L’ordre dans lequel la matrice affiche les permutations souligne la présence de deux sous-groupes. Le premier, formé par les transformations {I, A, B, C}, est isomorphe au groupe de Klein. Une correspondance s’établit entre les transformations {I, A, B, C} et {O, R, I, IR}. Elles possèdent la même structure et ne diffèrent que par leur notation. Le deuxième sous-groupe est constitué des transformations (I) à (L2). Il forme le groupe alterné A4.
La théorie des groupes permet à Xenakis d’organiser des cycles de permutations selon un système. Elle entraîne une structuration des caractéristiques sonores semblable à celle qui se produit avec la théorie des cribles. Cependant, alors que la théorie des cribles repose sur une seule dimension, dans la plupart des cas, soit l’axe des hauteurs, soit l’axe du temps, les groupes de permutations en nécessitent deux : une structure « hors-temps » qui définit les éléments du groupe, et une structure « temporelle », cinématique, qui détermine l’enchaînement de ces éléments. Une fois constitué l’ensemble des éléments qui forment un groupe, Xenakis définit un processus qui engendre l’ordre dans lequel les éléments se succèdent. Dans la plupart des cas, les transformations du groupe choisi s’enchaînent par produit : chaque transformation est le résultat du produit des deux transformations précédentes. Par exemple, à l’intérieur du groupe de permutations P4, à la suite des transformations (A) et (D) survient celle qui correspond au produit de (A) et (D) : (L2), puis (E), (C), etc. Ce processus engendre une série de voies cycliques. Le groupe des permutations de 4 éléments compte 70 voies de différentes longueurs, qui peuvent être regroupées en 12 classes. Puisque les voies forment des cycles, le début de chaque voie est arbitraire.
Remarques
This text has been adapted from Gibson, Benoît. 2011. The Instrumental Music of Iannis Xenakis: Theory, Practice, Self-Borrowing. Iannis Xenakis Series, No. 3. Hillsdale, N.Y. : Pendragon.
Sources
- Ledermann, Walter. 1964. Introduction to the Theory of Finite Groups. Edinburgh and London: Oliver and Boyd.
- Xenakis, Iannis. 1990. « Originality in Musical Composition. » IN Technology’s Challenge for Mankind, edited by the Steering Committee of the Fukushima International Seminar, Tokyo: Technova.
- Xenakis, Iannis. 1992. Formalized Music. Thoughts and Mathematics in Music. Hillsdale, New York: Pendragon.
Citer cet article
GIBSON, Benoît. 2023. “La théorie des Groupes” In A Xenakis Dictionary, edited by Dimitris Exarchos. https://www.iannis-xenakis.org/en/group-theory
