James Harley
Le concept et la technique de l’arborescence sont nés après que Xenakis eut écrit et publié des textes importants sur sa musique. Il a commencé à y travailler au début des années 1970, à peu près au moment où Formalized Music a été publié sous sa forme anglaise et élargie (Xenakis 1971). Le concept n’est cependant pas nommé pas dans cet ouvrage. Sous une forme latente, Xenakis a peut-être pensé à l’arborescence en travaillant sur Synaphaï (1969) pour piano et orchestre. Cette œuvre explore ce qu’il appelle la « contiguité » (voir la préface de la partition), et l’écriture linéaire pour le soliste va jusqu’à noter des portées séparées pour chaque doigt. Sa discussion la plus détaillée sur les arborescence sse trouve dans le livre d’entretiens avec Bálint András Varga. Publié en 1996, ce livre est écrit sur des bases de conversations tenues en 1980 et 1989. L’explication commence par la notion de point. Dans le temps, un point se répète pour affirmer sa présence, formant une ligne. Il est concevable que les valeurs qui composent cette ligne changent, éventuellement sous l’effet d’une marche aléatoire, dont la forme la plus élémentaire consiste à choisir au hasard une valeur voisine. En d’autres termes, si la valeur du point est fixée à zéro, les valeurs voisines seront 1 ou -1. La possibilité de modifier la valeur de la ligne de point permet d’obtenir différentes trajectoires. Des processus aléatoires plus sophistiqués, basés sur des fonctions mathématiques stochastiques, produiront des résultats plus variables, même en agissant sur un point de départ simple. Une ligne (tronc) peut générer une structure arborescente à la suite d’itérations du processus génératif. Comme le dit Xenakis
en partant d’un point, nous avons atteint un buisson ou même un arbre . Cela peut se produire librement, mais aussi selon des règles, et peut devenir aussi complexe que la foudre ou les veines du corps.
Varga 1996, 88
Xenakis a développé une base théorique pour cette approche, sans doute grâce à sa formation d’ingénieur (bien qu’il n’ait pas publié de traitement approfondi des arborescences). L’un des concepts sur lesquels il s’est appuyé concerne les transformations topologiques.
Il s’agit d’une transformation continue, […] ou d’un homéomorphisme, […] une correspondance biunivoque entre les points d’une figure et les points d’une autre figure, de sorte que des points arbitrairement proches sur une figure se transforment en points également arbitrairement proches sur l’autre figure.
The Columbia Electronic Encyclopedia, “Topology: Continuous Transformations and Equivalent Figures”
Les marches aléatoires et les transformations topologiques ont jeté les bases de la technique de l’arborescence. Une grande partie du travail de Xenakis a toutefois été réalisée par le biais de croquis et de dessins graphiques, qui ont ensuite été transposés dans le domaine du son. Il convient de noter que son travail sur l’arborescence a eu lieu à peu près au même moment où il développait son système d’informatique musicale graphique, l’UPIC, qui a été dévoilé en 1978. L’UPIC permet à l’utilisateur de dessiner des sons sous forme de graphiques qui sont transformés en sons directement, sans avoir recours à la notation musicale.
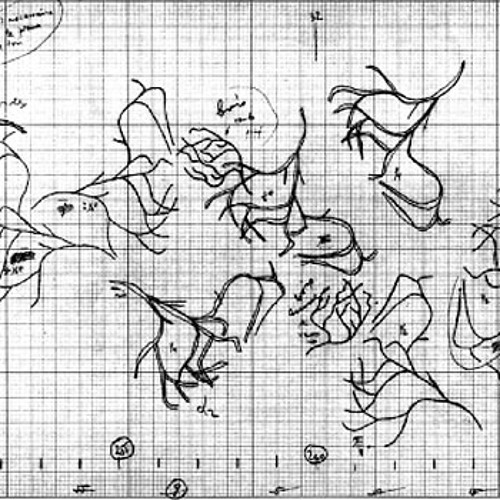
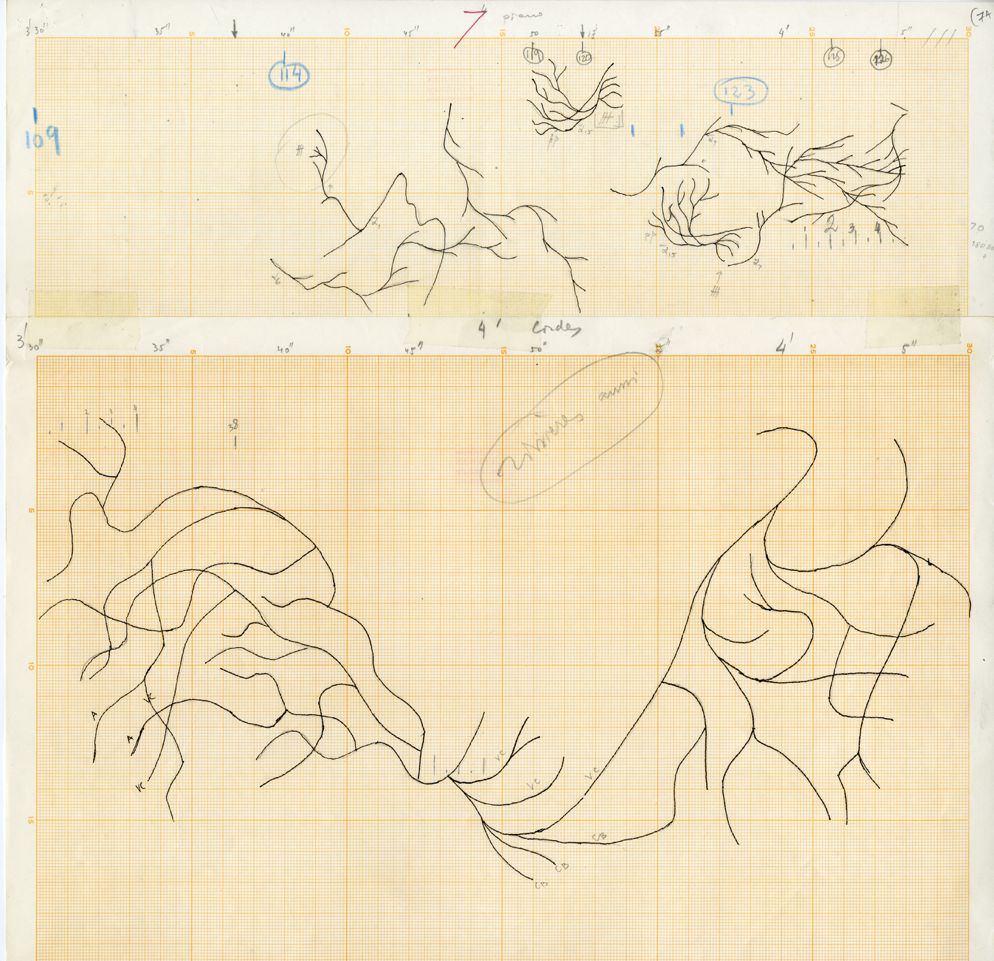
Pour Erikhthon (1974) pour piano et orchestre, Xenakis a créé un certain nombre d’esquisses graphiques qu’il a ensuite transcrites en musique. Cet exemple montre clairement des formes arborescentes ; l’une d’entre elles a été reproduite plusieurs fois, chaque fois sous un angle et à un endroit différents. L’organisation du dessin est clairement visible à l’œil nu, mais elle peut être plus difficile à percevoir sur le plan sonore. En effet, la transposition en sons fait apparaître les hauteurs sur l’axe vertical et le temps sur l’axe horizontal. Dans certains cas, l’arborescence peut produire des accords plutôt que des mélodies, en raison de la manière dont le dessin s’inscrit dans l’espace hauteur-temps. D’une certaine manière, le compositeur nous met au défi, nous les auditeurs, d’apprendre à reconnaître l’identité des formes dans le son. Cette démarche est liée à la notion plus traditionnelle de reconnaissance d’une mélodie qui a été inversée ou présentée de manière rétrograde. L’autre question intéressante concernant le transfert sonore découle de la manière dont les dessins sont transcrits en musique. Pour les instruments à cordes, en l’occurrence ceux de l’orchestre, les dessins peuvent être traduits en sons au moyen de glissandi continus. Pour le piano solo, les formes doivent être reportées sur une grille, le dessin continu étant échantillonné à la résolution des notes chromatiques du piano, ou aux divisions temporelles du temps représentées par les battements et leurs divisions.
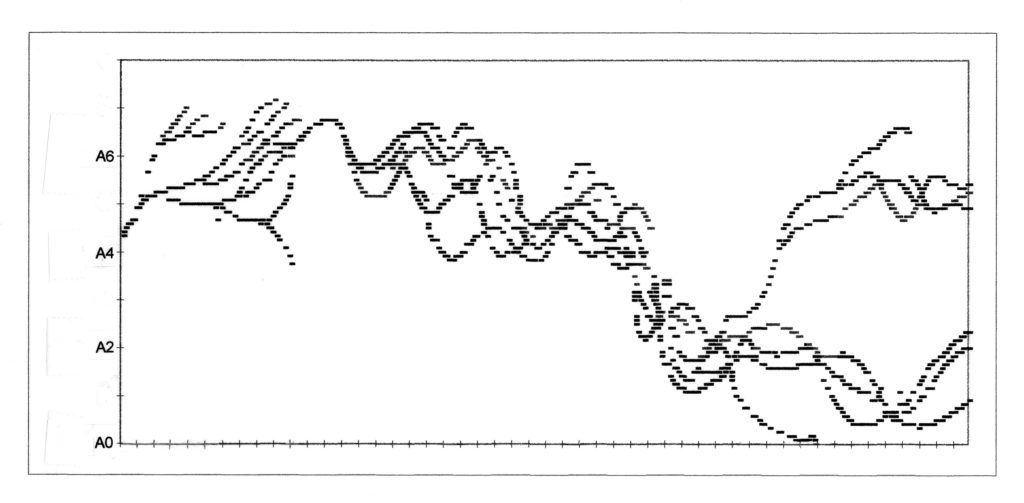
Dans cette transcription graphique d’Evryali (1973) pour piano solo, le dessin montre comment une seule ligne peut proliférer, produisant jusqu’à six lignes indépendantes. Ces lignes ont pu être produites en appliquant un processus mathématique de marche aléatoire contraint, ou par une esquisse graphique. Quoi qu’il en soit, le résultat est une nouvelle forme de contrepoint, un moyen de créer des textures musicales linéaires. Xenakis s’est inspiré des arborescences, formes linéaires proliférantes, dans de nombreuses œuvres ultérieures, dont Jonchaies (1977) pour orchestre, Mists (1980) pour piano solo et Tetras (1983) pour quatuor à cordes. Selon le compositeur
Xenakis drew on arborescences, proliferating linear shapes, in numerous subsequent works, including Jonchaies (1977) for orchestra, Mists (1980) for solo piano, and Tetras (1983) for string quartet. According to the composer,
l’idée d’arborescence est étroitement liée à la causalité, à la répétition et donc à la variation
Varga 1996, 88
Elle est donc liée à l’idée de continuité, de mouvement linéaire et de croissance ; la poursuite d’une idée générative est fondamentalement basée sur des aspects de son état actuel qui prennent vie en affirmant son existence dans le temps et en évoluant selon des principes stochastiques ou par intuition-conception
Références
The Columbia Electronic Encyclopedia, 6th ed. (2023), Columbia University Press, s.v. “Topology: Continuous Transformations and Equivalent Figures,” https://www.infoplease.com/encyclopedia/science/math/basics/topology/continuous-transformations-and-equivalent-figures
Harley, James. 2004. Xenakis: His Life in Music. New York: Routledge.
Varga, Bálint András. 1996. Conversations with Iannis Xenakis, London: Faber and Faber.
Xenakis, Iannis. 1971. Formalized Music, Bloomington, Indiana University Press.
Citer cet article :
HARLEY, James. 2023. “Arboresence.” In A Xenakis Dictionary, edited by Dimitris Exarchos. https://www.iannis-xenakis.org/en/arborescence